Diffraction is when a wave spreads out as it passes through a small slit or any intricate surface. With Photography, this would apply to how the light interacts with the aperture and how the photosites detect it on a sensor.
When light is focused through the aperture, it interacts with the edge of the aperture blades causing it to spread out where its angle bends slightly, this causes a reduction with the maximum optical resolution. The smaller the aperture the greater the effect. You can see a visible real-world example in a harbor or a pond by watching a wave as it bends around a jetty.
Diffraction Calculator
How will diffraction affect your camera?
Use this diffraction calculator to see the limits of diffraction on any given sensor with any number of megapixels.
*This calculator is based on a standard Bayer sensor. New technology like that found in BSI sensors has removed the circuitry. Gaps between the pixels continue to be improved or are compensated with microlenses as technology advances. New sensor advancements allow for an actual larger pixel pitch, which is why you usually see a jump in resolution when sensors upgrade to BSI.
Diffraction | The Equation
The Airy Disc
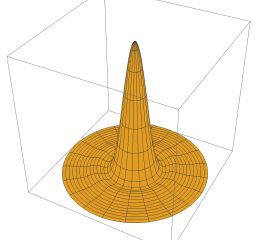
In optics, we look at diffraction through the Airy Disc or Airy Pattern. A circular pattern named after George Biddell Airy. This doesn’t necessarily reflect what the light is doing in terms of the shape, rather it’s the spread of a power vector. This illustrates that about 84% of the power of the wave is in the first cone and 91% within the first and second cones. This means that the majority of an image resolution is made up of the diameter of the first cone, which can also be referred to as the circle of confusion.
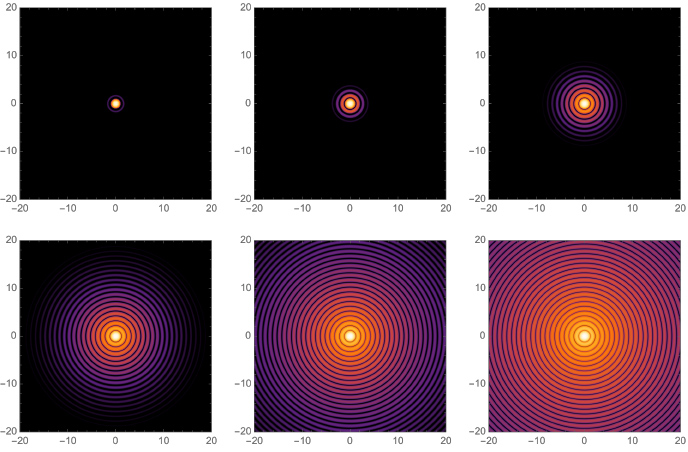
To put it the simplest way possible, as your aperture gets smaller, diffraction causes the Airy Pattern to get larger, and when the diameter is about 2.5x larger than a single pixel on a sensor, there will be a visible reduction in optical resolution.
If you were to shine a laser through an aperture and close that aperture down, you would get a pattern on a wall that looks like this – rendered with Mathematica.
How Aperture Can Ruin A Shot
The smallest spot of detail a lens can produce is 2.44 x Fstop x λ.
Your aperture will have a direct role in the details your lens can produce. For example, if you were to shoot at f19, your smallest spot of perfect detail produced (the Airy Disc diameter) would be (2.44 x 19 x 0.5) = 23.18 microns.
A look at diffraction at various apertures.
Calculations are taken between 0.4 and 0.6 since that is the range of the visible light spectrum.
| F-Stop |
Diffraction Size 0.4-0.6λ (microns) |
Average 0.55 λ |
Circle of Confusion |
| f19 | 18.54 – 27.82 | 25.5 µm | 7.4 – 11.13 |
| f16 | 15.62 – 23.42 | 21.5 µm | 6.25 – 9.36 |
| f11 | 10.74 – 16.10 | 14.7 µm | 4.3 – 6.44 |
| f8 | 7.81 – 11.71 | 10.7 µm | 3.12 – 4.68 |
| f5.6 | 5.47 – 8.20 | 7.5 µm | 2.19 – 3.28 |
| f4 | 3.90 – 5.87 | 5.3 µm | 1.56 – 2.35 |
| f2.8 | 2.73 – 4.10 | 3.7 µm | 1.09 – 1.64 |
| f2 | 1.95 – 2.93 | 2.7 µm | 0.78 – 1.17 |
It may look like at f2.8, your diffraction limit is 2.73 – 4.09 microns in size. However, the Airy Disk pattern doesn’t have hard edges and visible light has a range of about 0.4 microns. When we look at the airy disc, about 84% of the power of the light will be within the first cone which creates a circle of confusion of about .4 of the airy disc, so there is a lot more room to play with before noticing diffraction and the range would really look more like 1.09-1.64.
Since light has a range in microns of about .4 microns, if you were shooting an image that was primarily blue, you would see less diffraction than if you were to shoot an image that was primarily red.
Diffraction | Real-World Results
How does this relate to our camera sensor and megapixels, and what does diffraction look like in a real-world shoot?
Here is a sample of how diffraction affects the rendering of the Zeiss 35mm f2.8 on the Sony A7r.

How Megapixels Play A Roll
When it comes to megapixels, they can play a roll in overall resolution. The size of the sensor and the number of megapixels determine the size of the pixels on the sensor.
A camera like the Nikon D800 with 36.3 megapixels has a pixel pitch of 4.878. This means that a single pixel is 4.878 microns in size.
If you were to shoot at f19, the smallest spot of perfect detail (the entire airy disc) you could produce is 23.18 microns and the circle of confusion (perceived resolution) would be 9.2 microns.
To maximize the use of the D800 sensor, which is capable of capturing the detail of 4.878 microns in size, you would need to shoot at an aperture of f9.5 or lower, which would produce an Airy Disk of 4.9 microns in size.
This is often why you see some camera manufacturers say that there is a limit to the number of megapixels a camera should have for general use. Too many megapixels means the diffraction limitation will meet the spherical aberration limitations, making it very difficult actually to capture more detail.
Pixel Sizes (In Microns) Based On Megapixels
Sensor sizes have been rounded to produce a close estimate. Canon full-frame is actually 36mm, but the Canon APS-C is actually 22.2mm, whereas the Sony APS-C is 23.6mm.
| Megapixels | Medium Format (53.90mm) | Full Frame (36mm) | APS-C (23.6mm) | Micro 4/3 (17.3mm) | 1/3″ (iPhone) |
| 50MP | 6.60 | 4.16 | 2.73 | 2.12 | — |
| 42MP | 7.20 | 4.53 | 2.97 | 2.31 | — |
| 36MP | 7.78 | 4.90 | 3.21 | 2.50 | — |
| 32MP | 8.24 | 5.20 | 3.41 | 2.65 | — |
| 28MP | 8.82 | 5.55 | 3.64 | 2.83 | — |
| 24MP | 9.53 | 6.00 | 3.93 | 3.06 | — |
| 22MP | 9.95 | 6.26 | 4.11 | 3.19 | 0.87 |
| 18MP | 11.00 | 6.93 | 4.54 | 3.53 | 0.98 |
| 16MP | 11.67 | 7.35 | 4.82 | 3.75 | 1.04 |
| 12MP | 13.47 | 8.49 | 5.56 | 4.33 | 1.2 |
Compare those numbers to the resolution limits at certain apertures and you can see how your lens aperture and diffraction will limit your resolution. At some point, packing more pixels onto a sensor quickly becomes futile.
How Cameras Are Designed Around The Diffraction Limit
Many high-megapixel cameras are designed to resolve perfect details between f5.6 and f8, the sweet spot of most lenses.
While it makes sense for the camera to try to take the megapixel count to the limits of diffraction, some cameras are designed well below the f5.6-f8 limits of diffraction with bigger photosites so they can perform better in low light and with video. Cameras like the Sony A7III and A7sIII for example.
Many smartphones have high-resolution cameras that lock the aperture to a certain f-stop on the camera so that the output of the lens will match the pixel pitch of the photosites on the sensor.
How Lenses Work With Diffraction
Different lenses will also produce different levels of diffraction. This may be related to the point of convergence or the aperture location within the design. The further the sensor is from the point of diffraction, the more the light has a chance to spread.
How Diffraction Can Affect Your Photography
You should be able to see how your aperture and sensor resolution work together. While owning a 50-megapixel camera is great, you’ll have to open up your aperture to fully take advantage of it. This is great for studio and wedding photographers, but not so great for landscape photographers.
When shooting at f8-f16, you likely won’t really see the difference between a 50-megapixel camera or a 42-megapixel camera. Sure, your images will have a larger dimension in size, but the detail should be very close to the same when scaled to match.
Diffraction is even less of a problem if you don’t print to the maximum size of the sensor output.
Why Larger Sensors Are Better
Larger sensors can pack in more megapixels and still come out with a larger pixel pitch. So a 50-megapixel medium format camera will always have an advantage over a 50-megapixel full-frame camera when shooting at higher apertures. The same applies to full frame compared to APS-C.
The Beauty Of More Megapixels
Based on diffraction and sensor microns, you might be thinking that having more megapixels is completely pointless. However, there are some advantages when it comes to image artifacts.
Having a 50-megapixel image and scaling down to 24 megapixels will do a great deal to help eliminate artifacts while still maintaining a very sharp image, compared to a 24-megapixel camera that uses an optical low pass filter to help eliminate artifacts. While optical low pass filters help reduce moire and artifacts, they lower the overall resolution.
In this case, a 50-megapixel camera with no optical low-pass filter shot at f11 should still look slightly better than a 24-megapixel camera with a low-pass filter shot at f5.6 even when they’ve both been scaled accordingly. Simply because the 50-megapixel image is scaling from more pixels, resulting in cleaner diagonal lines, whereas the 24-megapixel camera uses a filter that impacts resolution.
If you removed the optical low-pass filter from the 24-megapixel camera, the detail should be the same, but you would be at a disadvantage regarding moire and aliasing.
What Is Diffraction? | Conclusions
This seems all confusing, but ultimately, what you need to take away is that the more you stop down your aperture, the less detail your lens is capable of producing. This, in turn, can greatly reduce some of the advantages of using a higher-megapixel camera.
While having tons of megapixels packed into your sensor is great, you have to consider the trade-offs. APS-C cameras and Micro 4/3 cameras will be much more impacted by diffraction because of their small pixel size.
Real World Use
Because of diffraction on my Sony A7r III, I typically like to shoot my landscapes at f8 to f11. I know I’ll not be capture as much detail at f11 compared to f8 but that’s ok. F11 is good enough for me and I’m willing to trade more depth of field for slightly less IQ.
The other alternative is to focus on stack. Macro photographers have been doing this for years and if we really want to take advantage of massive megapixel cameras, landscape photographers will have to focus stack. Meaning, shooting at something like f5.6 at various focus ranges and blending the images in post. The other alternative is to invest in medium format cameras that have even bigger sensors with bigger pixels or wait for stacked sensors to become mainstream.
I’m not a math genius, but some people who read this will be (although I did finish my College Trig final in 15 minutes). If it looks like I have a mistake, please let me know.